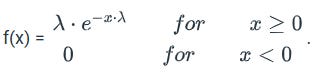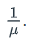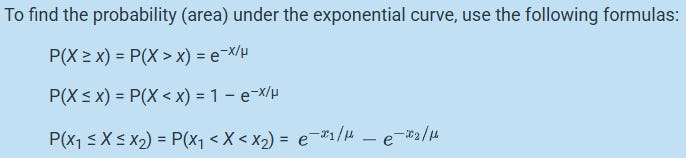6.3 Exponential Distribution

An exponential distribution models a continuous random variable over time, area or space where the rate of occurrences decreases as X gets larger.

The probability density function (PDF) for an exponential curve is

The value lambda λ is the fixed rate of occurrence and is equal to one divided by the mean:

If the mean is given in the problem then you write the PDF as f(x) = , where e is a mathematical constant approximately equal to 2.71828, x ≥ 0 and x is the value you are trying to find the probability for, μ is the mean number of a successes over an interval of time, space, volume, etc. The distribution is denoted as X~Exp(λ).

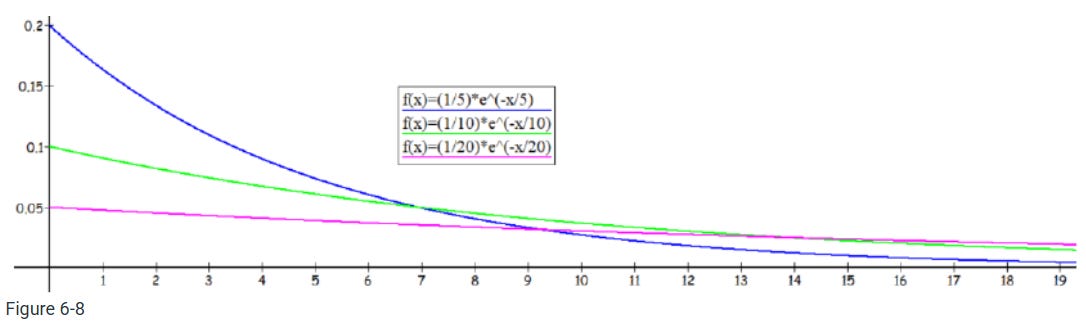
Figure 6-8 gives example graphs for a mean of 5, 10 and 20. Note the curve hits the y-axis at 1/μ and keeps going forever to the right with an asymptote at y = 0.

Example 6-2

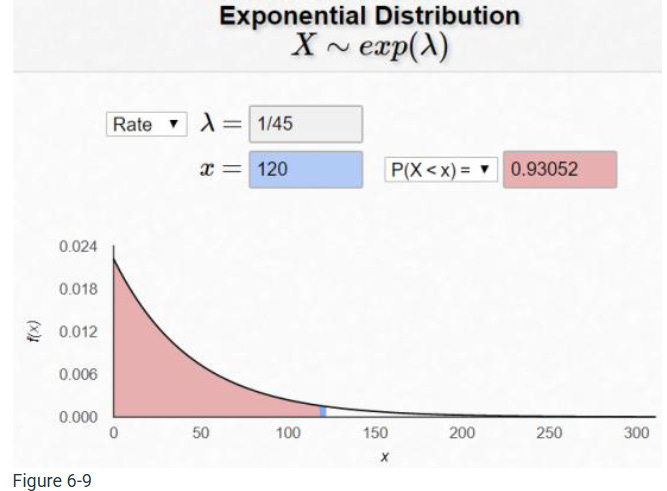
The time it takes to help a customer at the customer service desk is exponentially distributed with an average help time of 45 seconds. Find the probability that a customer waits less than two minutes.

Solution

We need to have the same units as the mean in the question so instead of finding P(X < 2 minutes) we will use P(X < 120 seconds). Also note that < and ≤ find the same probabilities so use the equation P(X < x) = 1 – e^–x/μ where x = 120 and µ = 45.

P(X < 120) = 1 – e^–120/45 = 0.9305.

In Excel use =EXPON.DIST(x,λ,TRUE) =EXPON.DIST(120,1/45,TRUE) = 0.9305.

Alternatively, as shown in Figure 6-9, the Exponential Distribution Applet/Calculator. will calculate the exponential probability.